
最不利荷载位置:使量值发生最大值(或最小值)的荷载位置。
1) 单个集中移动荷载
这是最简单的一种情况。影响线的最大与最小值点即为最不利荷载位置。
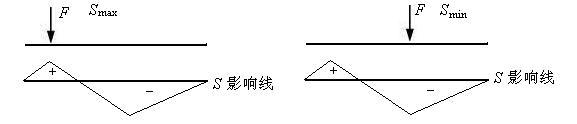
图11.19
2) 可任意断续布置的均布荷载
布满正号面积产生最大值,布满负号面积产生最大负值。
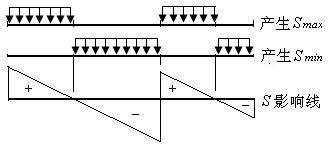
|
| 图11.20 |
3) 一组间距不变的移动集中荷载
难以直观判断,必须进行一定的分析计算。
图11.21
前面已证明,同一直线段上的各力可用其合力代替,有
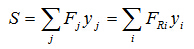
各直线段与x轴夹角a1,a2,…,an,逆时针为正。当荷载移动微小距离Dx时,有


极大值条件:
 时,
时,  ,
,  ;
; 时,
时,  , 即
, 即 变号.
变号.
极小值条件:
 时,
时,  ,
, ;
; 时,
时, , 即
, 即 变号.
变号.
即,在某个位置,当荷载向左向右有微小移动时, 变号,说明量值
变号,说明量值 在该处的极值。
在该处的极值。
什么情况下 会变号?只有当某个荷载作用在影响线的顶点上时才有可能。
会变号?只有当某个荷载作用在影响线的顶点上时才有可能。
不是每个荷载作用在影响线顶点上,都会使 变号。使
变号。使 变号的那个荷载称为临界荷载,此时的荷载位置称为临界位置。
变号的那个荷载称为临界荷载,此时的荷载位置称为临界位置。
临界位置可能有好几个,最不利荷载位置一定在临界位置之中。
最不利位置判别方法(试算法)
(1) 直观判断哪几个荷载有可能是临界荷载,逐一置于影响线的顶点上。
(2) 左移时,计算 ;右移时,再计算
;右移时,再计算 ,看其变号没?
,看其变号没?
若变号,是临界位置,计算此时的量值 ;若不变号,则不是临界位置。
;若不变号,则不是临界位置。
(3) 在几个临界位置中,比较各自的 值大小,可确定出最不利位置。
值大小,可确定出最不利位置。
【例11-6】 求图示简支梁在中-活载作用下 截面的最大弯矩值。
截面的最大弯矩值。

铁路普通活载
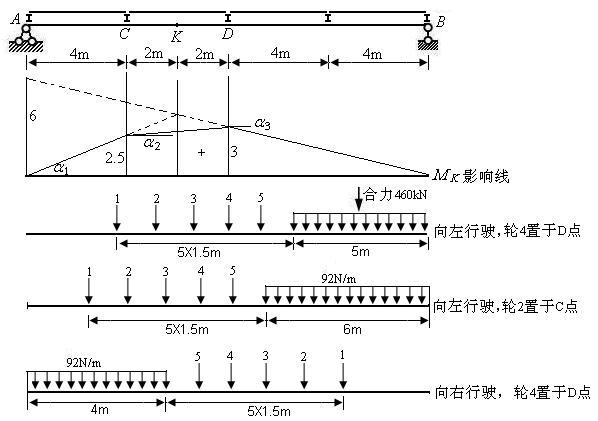
图11.22

4) 三角形影响线临界位置判别式
对于三角形影响线,临界位置的判别可简化。
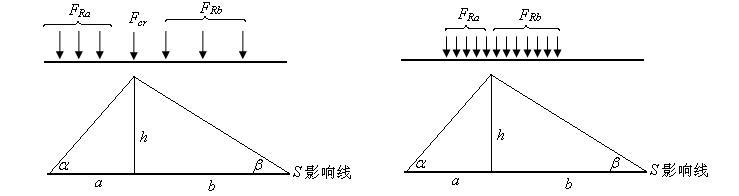 图11.23
图11.23
极大值条件是
左移,
右移,

 ,
, ,代入上面二式,得三角形影响线临界位置判别式为
,代入上面二式,得三角形影响线临界位置判别式为
 ,
, ,即
,即 记入哪一边,那一边平均荷载就大些。
记入哪一边,那一边平均荷载就大些。
 是举足轻重的。
是举足轻重的。
对于均布荷载, 是连续变化,导数存在,极值条件为一阶层导为0,有
是连续变化,导数存在,极值条件为一阶层导为0,有
 ,
, , 即,
, 即, , 左、右两边平均荷载相等。
, 左、右两边平均荷载相等。
【例11-7 】图示简支吊车梁,受到两台吊车荷载的作用,已知轮压 ,
, 。试求
。试求 截面最大弯矩。
截面最大弯矩。
先作出 影响线,直观判断
影响线,直观判断 、
、 不是临界荷载。
不是临界荷载。
·  置于C点,
置于C点, ,
,  ,是临界位置,
,是临界位置, kN.m
kN.m
·  置于C点,
置于C点, ,
, , 也是临界位置,
, 也是临界位置, kN.m
kN.m
故, kN.m
kN.m
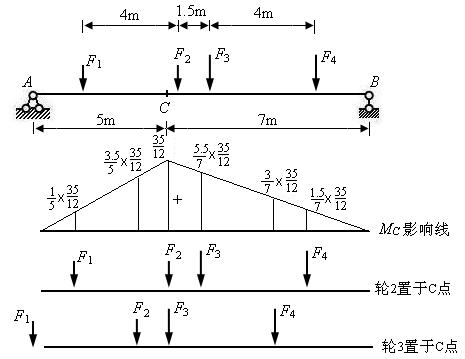
图11.24
 换算荷载*
换算荷载*
铁路与公路标准荷载制中,规定了多种标准移动荷载。结构设计时,求某量值最大或最小值,每次都要试算,从临界位置中找出最不利位置,很麻烦。
为简化计算,实际工作中,是利用已经缝制好的换算荷载表,查表进行计算,很方便。
换算荷载:已知结构某量值S 影响线,某种移动荷载作用下,最不利位置下,产生Smax。换算荷载是一种等效均布荷载K,即在K 的作用下,产生量值的大小正好也是Smax。
即换算荷载K ,与实际移动荷载在最不利位置上作用的结果相同。显然,查表查出K ,立即就可求出Smax。

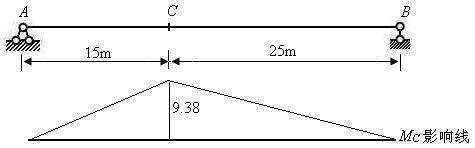
图11.25
【例】:简支梁,汽车-10级荷载作用下, kN.m,相应的换算荷载为
kN.m,相应的换算荷载为

 /
/ 中-活载作用下,
中-活载作用下, kN.m,相应的换算荷载为,
kN.m,相应的换算荷载为, kN/m
kN/m
换算荷载 与影响线形状有关。可以证明,对于竖标在固定比例的各影响线,其换算荷载相等。
与影响线形状有关。可以证明,对于竖标在固定比例的各影响线,其换算荷载相等。
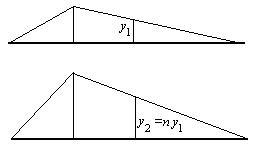
图11.26
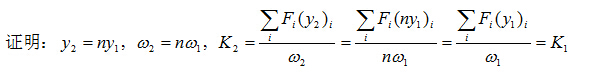
所以,只要三角形影响线底边长度相同,顶点位置相同,换算荷载就相同。
对于三角形影响线,中-活载的换算荷载, 见教材P303表11-1:
(1) 表是根据三角形影响线制成的;
(2) 加载长度 ,指同符号影响线的长度,也就是三角形影响线底边的长度;
,指同符号影响线的长度,也就是三角形影响线底边的长度;
(3) 三角形顶点的位置:用参数a表描述, 指顶点到较近零点的水平距离
指顶点到较近零点的水平距离
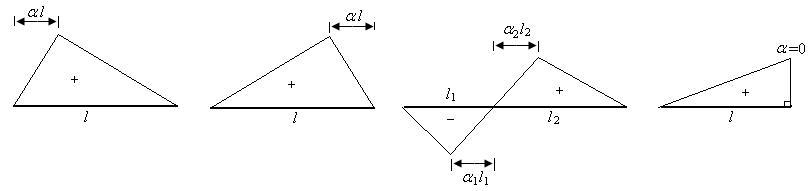
图11.27
(4) a、 值表中没有时,利用插值计算出相应的K 值。
值表中没有时,利用插值计算出相应的K 值。
【例11-8】 图示简支梁,中-活载作用下,求 ,
, ,
,
先作出 与
与 的影响线。
的影响线。
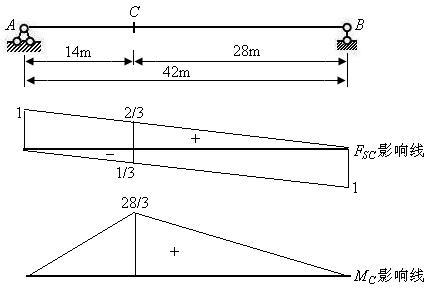
图11.28
(1) 求 ,
, ,
,  , 查表得
, 查表得  kN/m,
kN/m,
 kN.
kN.
(2) 求 ,
,  , a=0, 查表没有,插值,
, a=0, 查表没有,插值,
 ,a=0,
,a=0,  kN/m;
kN/m;  , a=0,
, a=0,  ;
; , a=0,
, a=0, kN/m;
kN/m;
 ,
,  kN/m,
kN/m, kN.
kN.
(3) 求 ,
,  ,a=1/3=0.333, 查表,没有,插值计算,得,
,a=1/3=0.333, 查表,没有,插值计算,得, kN/m
kN/m
 kN.m
kN.m
