结构通常由若干杆件组成，其最基本的功能就是承载，但并非所有的杆件体系都能承载。

几何不变体系：不考虑杆件本身的变形，任意荷载作用下，其几何形状与位置均能保持不变，这样的体系称为几何不变体系。显然，结构必须是几何不变体系。

几何可变体系：在很小的荷载作用下，也会发生机械运动，而不能保持原有的几何形状和位置，这样的体系称为几何可变体系，或机构。

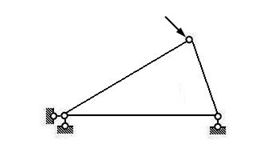
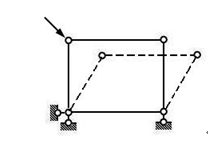
(a)几何不变体系	(b) 几何可变体系

                                          图2.1

判别一个体系是否几何不变体系，从而确定其能否作为一个结构在工程上应用，称为机动分析，或几何构造分析，或几何组成分析。

刚片：机动分析中，不考虑材料本身的变形，所以，一根杆件，或一个已知的几何不变部分，都可以看成是一个刚体，二维的刚体就是刚片。

                                                    平面体系的计算自由度

自由度：确定物体位置所需的独立坐标的数目。

判别一个体系是否几何可变，可先计算一下它的自由度w，若w>0，则体系必然是几何可变的。

约束：限制体系运动的装置称为约束。凡是减少一个自由度的装置，称为一个约束。

(a)平面上的一个点，2个自由度	(b)  刚片，3个自由度	(c) 1根链杆约束，是1个约束
(d)1个单铰约束，是2个约束	(e) 连接n个刚片的复铰，相      当于n-1 个单铰	(f)刚结点是3个约束
图2.2

实际自由度：体系实际具有的自由度。

计算自由度w ：通过计算而得出的体系的自由度。

计算自由度与实际自由度有时不一致。

如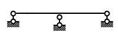，，w =0, 实际自由度为1. w >0可以肯定体系必为可变体系。w =0或 w<0，则不能说明体系的机动性质。但通过计算自由度，可得出一些有用的信息。

(1) w > 0，缺乏必要约束，几何可变。

(2) w =0，具有必要的约束数目，但是否几何不变还要看约束是否恰当。

(3) w < 0，具有多余约束，但是否具有必要的约束还未知。

求计算自由度w有两种方法，刚片法与铰结点法。

平面体系 = 刚片+ 约束(铰约束、支座约束)

有个刚片个单铰(包括单铰与由复铰换算出的单铰数)，个支座约束

个自由度   个单铰等于个约束

则有

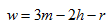
【例2-1】

 图2.3

【例2-2】

                                       图2.4

，一个是几何不变，一个是常变体系。

适用于结点全部都是铰结点的铰接体系。

平面体系=铰结点(j个) + 链杆约束(b个) + 支座约束(r个)

     如，上页的例2-2，,,,.