
| 种类有 |
|---|

|
| (a) 简支梁 | (b) 伸臂梁 | (c) 悬臂梁 | (d) 不常用,受力不好,但为静定 |
| 图3.1 静定单跨梁 |

1.反力的计算

取全梁为隔离体,由全梁整体平衡条件, ,
, ,
, ,即可求出三个支座反力。一般情况下,梁仅受竖向荷载作用,无水平反力,这是梁结构的一个重要特点。
,即可求出三个支座反力。一般情况下,梁仅受竖向荷载作用,无水平反力,这是梁结构的一个重要特点。

2.截面法求指定截面的内力

在指定截面处切开,取隔离体(左边或右边部分),由平衡条件求出切开截面上的内力。
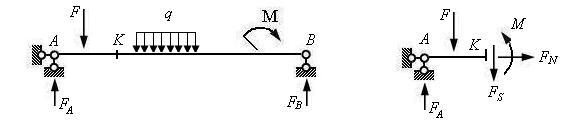
图3.2,不用列出平衡方程,可直接进行代数运算求出截面上的内力值
内力符号规定: ,使梁下侧受拉为正;
,使梁下侧受拉为正; ,拉力为正;
,拉力为正; ,绕隔离体顺时针为正。
,绕隔离体顺时针为正。

3.荷载与内力的微分关系

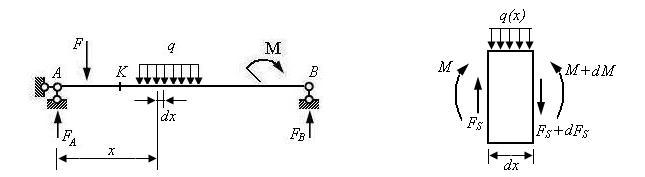
图3.3
以微段dx为隔离体,SY=0,得出
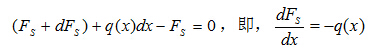
对微段右截面列出力矩平衡方程,有
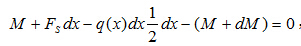 略去二阶微量,有,
略去二阶微量,有,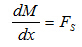
即
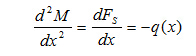
讨论:
(1) 无荷载段, ,FS =C (水平线),
,FS =C (水平线), (斜直线,
(斜直线, /
/
 ,其斜率为剪力FS )
,其斜率为剪力FS )
(2) 均布荷载段, ,
, (斜直线),
(斜直线), (二次抛物线),
(二次抛物线), /
/ 处,
处, 图有极值。
图有极值。
(3) 铰支座(铰结点)处,
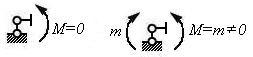
图3.4
(4) 集中力作用处
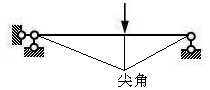
图3.5
M左=M右, 图在集中力作用处连续。
图在集中力作用处连续。
FS右 FS左,FS右
FS左,FS右 FS左=F ,
FS左=F , 图在集中力作用处有突变,突变大小即为
图在集中力作用处有突变,突变大小即为 ;
; 为
为 图的斜率,集中力作用处,剪力不连续,即
图的斜率,集中力作用处,剪力不连续,即 图的斜率不连续,
图的斜率不连续, 图有尖角,如
图有尖角,如
(5) 集中力偶作用处
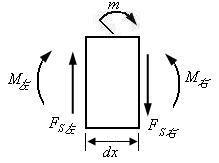
图3.6
FS左=FS右,FS 图在集中力偶作用处连续。
M右 M左,M右
M左,M右 M左
M左 ,
, 图在集中力偶作用处有突变,突变值为
图在集中力偶作用处有突变,突变值为 ;
; 为
为 图的斜率,集中力作用处,剪力不连续,即
图的斜率,集中力作用处,剪力不连续,即 图的斜率不连续,
图的斜率不连续, 图有尖角。
图有尖角。

4.内力图作法

(1) 以杆轴线为基线,垂直于杆轴线的竖标表示内力大小。
(2)  图,正值画在基线上面,负值画在基线下面,标大小,标正、负号。
图,正值画在基线上面,负值画在基线下面,标大小,标正、负号。
(3)  图,画在受拉的一侧,标大小,不标正、负号。
图,画在受拉的一侧,标大小,不标正、负号。
作图步骤:(a) 求反力;(b) 求出分段点上的内力值;(c) 分段作出内力图。
【例3-1】 作梁的 图与
图与 图。
图。
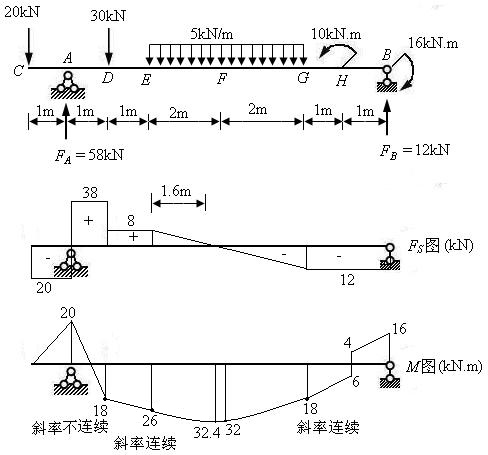
图3.7
(1) 求反力, ,得出,
,得出, ;
; ,得出,
,得出, ;校核,
;校核,
(2) 求出C、A、D、E、F、G、H、B 各点的 与
与 值;
值;
(3) 分段作出 与
与 图。
图。

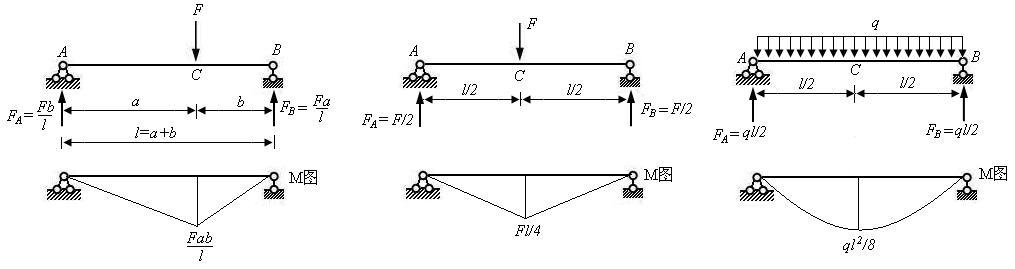
5.叠加法作M图

非常重要,基本功,一定要熟练掌握。
线弹性结构叠加原理:多个荷载共同作用的结果,等于各荷载单独作用结果的叠加。
先来看几种基本荷载作用下产生的 图(基本图形),再利用叠加法作复杂情况下的
图(基本图形),再利用叠加法作复杂情况下的 图。
图。
 图的基本图形:
图的基本图形:
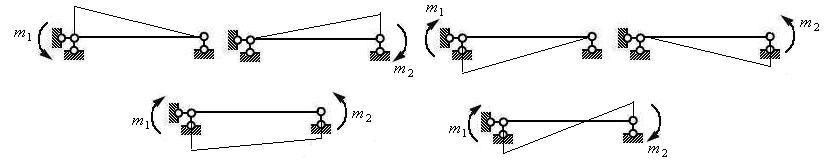
图3.8 |
铰支座处一般 为0,但当有力偶作用时,则 为0,但当有力偶作用时,则 为再为0. 为再为0. |
 |
| 图3.9 |
 |
| 图3.10 |
叠加法作 图,就是利用以上基本图形,作出复杂情况下的
图,就是利用以上基本图形,作出复杂情况下的 图。
图。

图3.11 |

图3.12 |
上面例3-1,图3.7中梁段EG,切出梁段EG单独分析,结构中任一梁段均可看成一简支梁,有
 图3.13 图3.13
|
【例3-2】叠加法作梁的 图 图
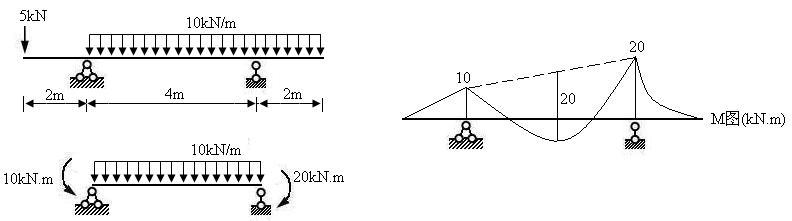
图3.14 |
【例3-3】叠加法作梁的 图 图

图3.15 |
