8.3(1)

8.3(2)

下面说明如何建立位移法典型方程。

    如下图示，位移法基本未知量包括刚结点1的角位移Z1与线位移Z2。Z1、Z2与荷载共同作用下，基本体系与原结构等效，则附加约束上的反力应该为0(因原结构上是没有附加约束的)，即

，

    说明刚结点1满足力矩平衡条件，意味着铰结点2满足水平方向力的平衡条件，它们实际上是结点的平衡方程。根据叠加原理，三种情况叠加后，有

(a) 原结构                      (b) 位移法基本体系

 

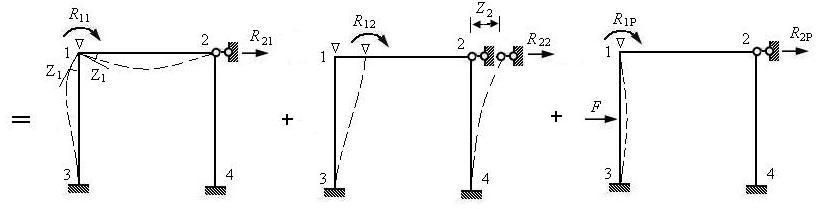
(c) Z1单独发生             (d) Z2单独发生             (e) 荷载单独作用

图8.10

表示引起的上附加约束的反力。引入刚度系数的概念，的定义为方向单位位移引起的方向上附加约束的反力，有

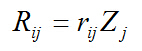
    因此

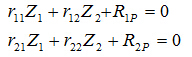
   上式称为位移法典型方程，其物理意义为基本体系在荷载与结点位移共同作用下，每一个附加约束上的反力为0，此时基本体系与原结构完全等价。位移法典型方程实质上是结构沿结点位移方向的平衡方程。

    对于具有个独立结点位移的结构，需要相应地施加个附加约束。根据每个附加约束上的附加反力或反力矩应为0的平衡条件，可建立位移法典型方程如下

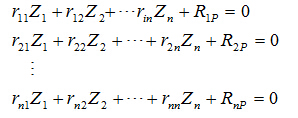
    在上述方程中， 称为主系数，其他系数  称为副系数，称为自由项。刚度系数与自由项的符号规定是，与结点位移方向一致为正。故，恒为正。根据反力互等定理有，,可正，可负，可为0。上式也称为结构的刚度方程，位移法也称为刚度法。

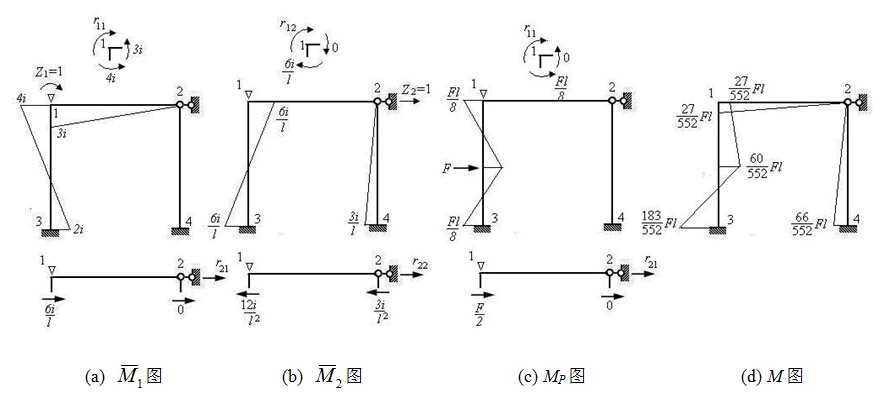图8.11

 

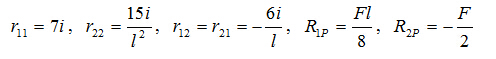
    上述结果代入位移法方程中，有

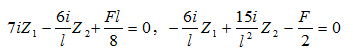
    解得

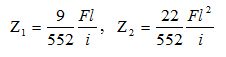
    Z1、Z2为正值，说明它们的实际方向与假设方向相同。

    依据叠加原理

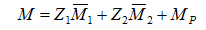
    可计算出最后的杆端弯矩值，如

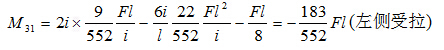
    其余杆端弯矩的计算依此类推。最后，可绘出原结构的 图。