位移法是将原结构离散成若干根单跨超静定梁，其杆端内力、杆端位移与其上作用荷载之间的关系是位移法中最基本的关系，用转角位移方程来表示，下面用力法来建立这种关系。

位移法中符号规定(重要)

与，与前面规定相同，拉力为正，绕隔离体顺时针为正。

，对杆端而言，绕杆端顺时针为正；对支座或结点而言，绕杆端或支座逆时针为正。

转角，顺时针为正

有三种基本的单跨超静定梁：两端固定梁，一端固定一端铰支，一端固定一端定向滑动。

1) 两端固定梁

首先考察两端固定梁，端转角为，端转角为，A、B两端垂直于杆轴线方向的相对线位移(简称为侧移)为，如图所示。

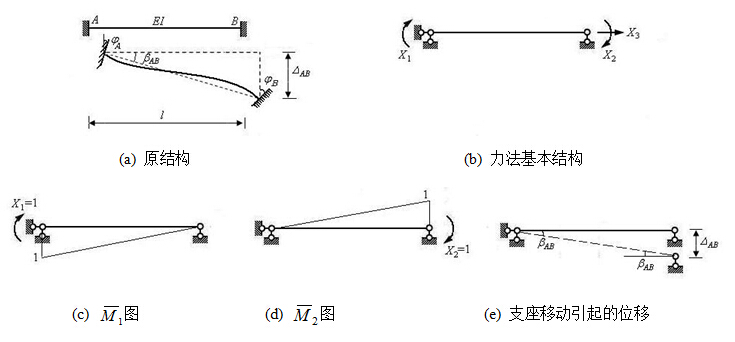
图8.2

用力法求解，多余约束力为、、，与梁的弯曲无关，故仅需求解、。原结构沿、方向的位移(即A、B端的转角)分别为、，故力法典型方程为

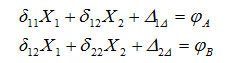
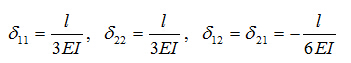
自由项、表示，基本结构上支座发生位移时，沿、方向产生的位移(即杆端A、B的转角)为，则

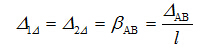
联立求解力法方程，有

令

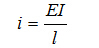
称为杆件的线刚度。另，用代替，代替，得到

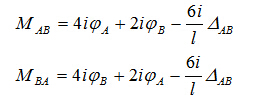
已知杆端弯矩，杆端剪力则不难通过杆件的平衡条件，即与求出

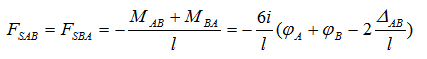
若两端固定梁除了发生上述支座位移外，同时还有荷载、温度变化等外界因素作用。荷载、温度变化等产生的杆端弯矩称为固端弯矩，记为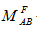    与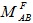(亦可用力法求解出来)。  最后的杆端弯矩，应为支座移动引起的弯矩与固端弯矩的叠加，即

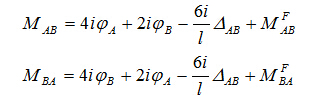
上式是两端固定等截面梁杆端弯矩的一般计算公式，通常称为转角位移方程。

2) 一端固定一端铰支的梁

    一端固定一端铰支的梁，显然 端弯矩为0，有

可解出，

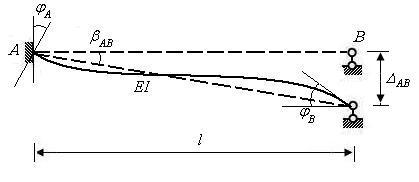
图8.3

由此知，铰支端的转角 可用与来表示，因而不是独立的结点位移。所以，在位移法中，铰结点或铰支座处的转角不作为求解的基本未知量。在表达式中消去 ，有

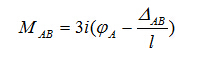
同样，由杆件AB的平衡条件，与，可求出杆端剪力

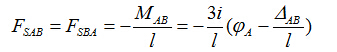
若考虑荷载、温度变化等产生的固端弯矩，则杆端最后弯矩应为支座移动产生的弯矩与固端弯矩的叠加，有

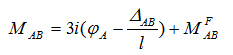
此即一端固定一端铰支梁的转角位移方程。

3) 一端固定一端定向滑动的梁

    一端固定一端定向滑动的梁，显然端剪力为0，有

可解出

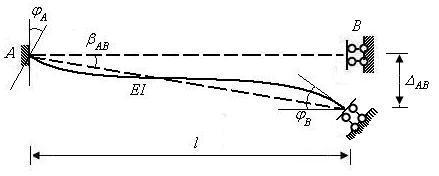
图8.4

由此可知，定向滑动端的线位移可用、来表示，因而不是独立的结点位移。所以，在位移法中，滑动端相对于固定端的侧移DAB不作为位移法的基本未知量，有

,

若还考虑荷载、温度变化等产生的固端弯矩，则杆端最后弯矩应为支座移动产生的弯矩与固端弯矩的叠加，有

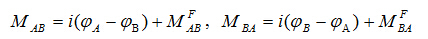
此即一端固定一端定向滑动梁的转角位移方程。

由三种单跨超静定梁的转角位移方程，可计算出单位杆端位移引起的杆端弯矩与剪力，及荷载作用与温度变化下产生的固端弯矩与剪力，具体结果列于P181表8-1中。

首先记住下面5项。

表5-1 单位杆端位移引起的等截面直杆的杆端弯矩与剪力(只记弯矩，剪力不用记)

编号	梁的简图	弯矩		剪力
1		4i	2i
2
3		3i	0
4			0
5		i	-i	0	0