‍下面通过几个例题，来掌握机动分析的方法与步骤。

【例2-3】

     图2.13

解(1)：基础上依次添加二元体；解(2)：从最右边开始依次拆除二元体。结论是几何不变无多余约束体系。

【例2-4】

 图2.14

去掉右端的二元体，几何不变有1个多余约束体系，1次超静定结构。

【例2-5】

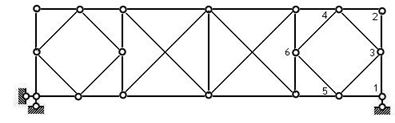
     图2.15

只有3根支座链杆，这种情况下可只分析体系本身。依次拆除二元体1、2、3、4、5，结点6处2根链杆处在同一直线上，瞬变体系。

【例2-6】 

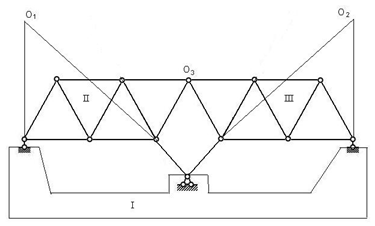
图2.16

                      

有4根支座链杆，不能去掉，只能连支座一起分析。三刚片规则，三个铰不共线，几何不变无多余约束体系。

【例2-7】

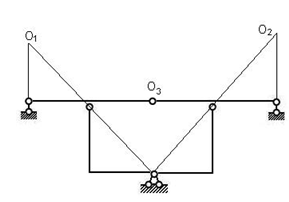
图2.17

三刚片规则，三个铰不共线，几何不变无多余约束体系。

 ‍

机动分析步骤：

‍‍(1) 当体系只有3根支座链杆与基础相连时，可去掉支座，只分析体系本身；

(2) 看外围有无二元体可拆除；

(3) 选取2或3个基本刚片，如果行不通可尝试不同的选取方案；

(4) 分析刚片之间的联结情况，看是否符合规则；

(5) 结论：几何不变无多余约束，几何不变有几个多余约束，瞬变体系，常变体系。

注意事项：所有杆件、支座、结点、包括基础等都要用上，不能遗漏，也不能重复利用。

‍【例2-8】 

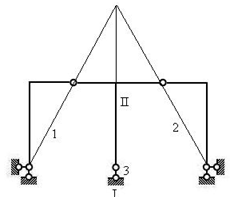
图2.18

二刚片规则，连接刚片I、II的3根链杆1、2、3汇交于同一点，瞬变体系。

【例2-9】

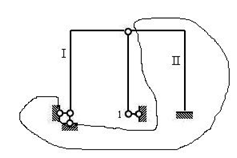
图2.19

去掉二元体1，刚片I、II之间用1铰与2根杆相连，几何不变有1个多余约束体系。

【例2-10】

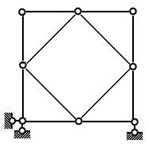
图2.20

从外围依次拆除二元体，常变体系。

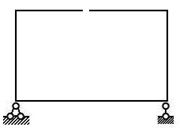
【例2-11】

(a)几何不变无多余约束	(b) 几何不变有1个多余约束	(c) 几何不变有2个多余约束

(d)几何不变无多余约束，同(a)	(e) 几何不变有3个多余约束

 图2.21    ‍‍

                                                    三刚片体系中虚铰在无穷远处的情况

无穷远虚铰：连接2个刚片的一对平行链杆，相当于将2个刚片在无穷远处铰接，称为无穷远虚铰。

1) 一个无穷远虚铰
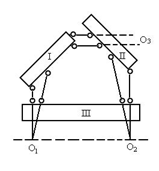(a)三铰不共线，几何不变	(b)三铰共线，瞬变	(c)三铰共线，平行且等长，常变

                                                   图2.22

组成无穷远铰的一对链杆，与另外两个铰的连线不平行，则三铰不共线，几何不变。‍

2) 二个无穷远虚铰
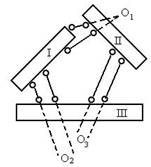
(a) 两对平行链杆之间不平行，三     铰不共线，几何不变	(b) 两对平行链杆之间又平行，瞬变	(c) 平行且等长，常变

                                               图2.23

3) 三个无穷远虚铰

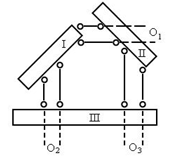
                                                  图2.24

(a) 三对平行链杆，三个无穷远虚铰，高等几何学中有定理，平面上所有的无穷远点均在同一条直线上。所以，这种情况下是三铰共线，瞬变体系。

(b) 三对平行链杆又各自等长，常变体系。‍

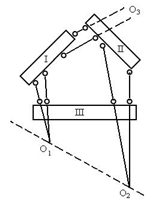
‍【例2-12】 

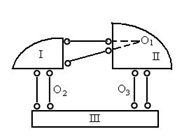
                                                  图2.25

(a) 基本刚片选取不当，无法分析，要换思路。

(b) 组成O₃的一对平行链杆，与O₁、O₂连线平行，三铰共线，瞬变体系。

                                                    几何构造与静定性的关系

常变体系：一般情况下，不满足静力平衡条件。不能承载。

瞬变体系：荷载作用下，内力无穷大，0荷载作用下，内力=0/0，为不定值。不能承载。

几何不变无多余约束体系：,, 方程数目未知力数目，静力平衡方程组有唯一一组解，静定结构。

几何不变有多余约束：,,方程数目未知力数目，静力平衡方程组有无穷多组解，超静定结构。